Что мы измеряем?
Уже много тысяч лет мы, сами того не подозревая, живем в мире цифр. Мы измеряем в цифрах все - один килограмм конфет, две шоколадки, пол-литра “жидкости” и др. При этом мы применяем так называемые “вещественные” единицы измерения - граммы, метры, ниты, атмосферы, литры и т.д.
Однако - как ни странно - существуют и весьма широко используются также и нематериальные единицы измерения, причем не только в ядерной физике, где их огромное количество - странность, очарование, цвет и др. - но и в обычной повседневной практике.
Об одной из таких единиц, причем “дважды экзотической” - децибеле - эта статья.
Почему же экзотической, да еще дважды?
Во-первых - не существует воплощенного “в металле” эталона децибела, его нельзя “повертеть в руках”, пощупать. Платино-иридиевые эталоны метра, килограмма - существуют, а децибела - нет.
Во-вторых, децибел - это не целая, а дольная единица. Мы часто пользуемся целыми (грамм, метр) иногда - кратными (КИЛОграмм, КИЛОметр), но практически никогда - дольными.
В самом деле - часто ли вы используете дециметр или дециграмм? Никому же не придет в голову сказать: "у меня дома потолки 27 дециметров”! Так откуда же взялась и для чего нужна сия малопонятная единица? Казалось бы: есть вольты, герцы, амперы... Чего еще желать? Однако - не так все просто! Посмотрите на два следующих рисунка:
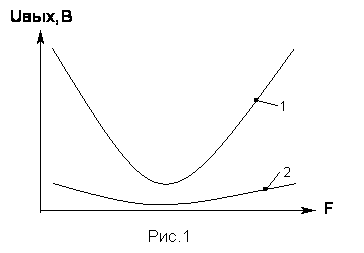
На рис 1 изображены две частотные характеристики.(На этом рисунке по вертикали отложено реальное выходное напряжение исследуемого устройства в вольтах).

Как видим, эти две АЧХ не очень-то похожи. Идем далее (рис.2):
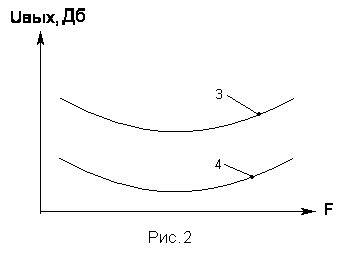
На рис 2 по вертикали отложены не вольты, а децибелы. Сразу стало видно, что эти характеристики идентичны, только одна находится чуть выше, а другая - ниже.
На самом деле все четыре характеристики принадлежат одному и тому же регулятору тембра, просто характеристики 1 и 3 снимались при подаче на его вход сигнала в 1Вольт, а 2 и 4 - 100 милливольт Очевидно что сравнение характеристик устройств по Рис.2 более удобно. Характеристики “в децибелах” не зависят от реальных физических величин сигналов, применяемых в процессе измерений. Это - одна из главных причин того, почему логарифмический способ отображения АЧХ получил наибольшее распространение.
Хотя на самом деле, помимо удобства чтения графиков, существует и другая, гораздо более существенная и глубокая причина: по закону Вебера-Фихнера между воспринимаемым ощущением и вызывающим его внешним воздействием имеется логарифмическая зависимость, т.е. чтобы ощущение изменилось “НА” какую-то величину, вызвавшее его воздействие должно измениться “В” раз.
Пояснить это можно на следующем примере: от 20 до 40 Герц -одна октава, и от 10000 до 20000 Герц -тоже одна октава. Только в первом случае частота изменилась на 20Гц, во втором - на 10000Гц, а результат - одинаков: и в том, и в другом случае частота изменилась “В” два раза и мы слышим повышение высоты звукового тона “НА” одну октаву. Таким образом, отображение данных в логарифмическом масштабе нам просто по-человечески “ближе”.
Ранее, довольно давно, в связи широкое применение получила единица НЕПЕР, основанная на натуральных логарифмах и названная в честь их изобретателя Дж.Непера (1550-1617г). 1 Непер соответствует изменению уровня сигналов в =2,718 раз (в “е” раз).
Вот это интересно! Непер существует давным-давно, а пользуемся - децибелом!
И почему именно децибелом, коль уже существуют натуральные логарифмы, а есть еще двоичные и т.д.? “Был ответ на тот вопрос прост...”
Применяемое для вычисления Неперовых логарифмов число “е” - число трансцендентное, и для расчетов крайне неудобное. Поэтому, по свойственной всем нам любви к круглым числам - логарифмы, имеющие в своем основании число 10, и получили более широкое распространение.
На десятичных логарифмах основан БЕЛ - единица, названная в честь изобретателя телефона А.Г.Бела. Однако, при ближайшем рассмотрении, он оказался “слишком крупным”, а вот одна десятая его -“децибел” - оказался в самый раз. Каким образом?
А вот каким: просто повезло. Децибел нам ближе по психофизиологическому восприятию. Один децибел (1 Дб) - это величина, максимально близкая к субъективному порогу восприятия - порогу различения громкости двух сигналов нашим ухом, и именно поэтому децибел занял ведущее место в звукотехнике.
Так как децибел - величина относительная, то с его помощью можно измерять все, что угодно - хоть музыкальные интервалы. Действительно, в одной октаве содержится шесть нотных интервалов, а изменению напряжений в два раза (как бы “на октаву”) соответствует изменение уровня на 6 Дб, т.е. музыкальный звуковысотный интервал в один тон - соответствует одному децибелу. Причем значения совпадают с точностью 0,0004.
Что это - глубинная, скрытая взаимосвязь? Как знать...
Однако, как уже упоминалось, децибел - величина относительная. А как быть,если надо измерять реальные физические величины - вольты, ватты и др?
Да очень просто: надо выбрать опорный (эталонный) уровень от которого и отталкиваться при измерениях. Давным-давно (так уж исторически сложилось) за опорный уровень была принята величина мощности в 1 милливатт на нагрузке 600 Ом. При этом величина напряжения составляет
![]()
где P=1 мВт - мощность; R=600 Ом - сопротивление.
До настоящего времени эта величина напряжения является опорной для подавляющего большинства измерений.
Однако иногда встречаются и некоторые другие величины. Опорная величина должна указываться после букв дБ. В английском языке приняты две основные величины:
обозначению dBu (русское-дБ) - соответствует опорное напряжение 0,775В; обозначению dBV (русское-дБв) - соответствует опорное напряжение 1В; встречается и обозначение dBm(дБм), для него опорный уровень - также 0,775В.
Как же пользоваться децибелами, как их вычислять?
Очень просто. Для расчета существует всего одна формула :
N=20 x lg(U2/U1),
где U1 - опорное напряжение; U2 - измеряемое напряжение;
N - их соотношение в децибелах.
При измерении мощности в этой формуле изменяется только одна цифра: первый множитель вместо "20" - заменяется на цифру “10”, а напряжения заменяются мощностью.
Если после расчета результат “N” получается со знаком “минус”, то это значит, что измеряемая величина меньше опорной (эталонной).
Все. На этом ВСЯ математика, связанная с понятием “децибел” - закончена.
Теперь немного о практическом значении некоторых параметров, выраженных (измеренных) в децибелах.
Некоторые наиболее распространенные уровни электрических сигналов:
Измерение уровней в звукотехнике
Казалось бы, что здесь сложного - измерить напряжение? Подключи вольтметр - и меряй себе на здоровье! Эх, если бы все было так просто! Так легко бывает, наверно, только у электриков. В звуке все гораздо сложнее…
Реальные звуковые сигналы похожи на все что угодно, кроме хорошо всем знакомой синусоиды. При измерении уровней звуковых сигналов результат будет зависеть как от характера анализируемой фонограммы, так и от типа применяемого вольтметра.
“Секрет” здесь заключается в том, что звуковой сигнал имеет ярко выраженный импульсный характер, со значительным пик-фактором. (Пик-фактором называется отношение мгновенной,”пиковой” амплитуды сигнала к его эффективному, действующему значению).
Пик-фактор очень сильно отличается у различных звуковых источников. Для нормально сведенной фонограммы (не “пережатой”) он составляет величину порядка 12 дБ, для речи 18-20 дБ, а уж для необработанной фонограммы, да еще для отдельных треков, а если для ударных... Даже подумать страшно!
Соответственно - и разные типы вольтметров на одном и том же сигнале будут давать различные показания.
Существуют три основных типа вольтметров - вольтметр “средних значений”, “пиковый” вольтметр и вольтметр “действующих значений”, иначе называемый “среднеквадратичный” (RMS).
Вольтметр средних значений (VU-meter, или “волюметр”) исторически появился самым первым, и является самым простым по устройству - показывающий прибор просто включен в диагональ диодного моста.
Динамические характеристики измерителя полностью определяются параметрами стрелочного индикатора, а все механические измерители имеют весьма значительный разброс по этим параметрам, соответственно и показывает он по преимуществу “цену на дрова на северном полюсе во время засухи”.
Однако - благодаря его длительному применению - звукорежиссеры накопили богатый опыт работы, позволяющий (при соответствующей практике) правильно оценивать показания измерителя и вносить необходимые поправки “на слух”, с учетом характера звукового материала. Только этим - и ничем иным - и объясняется такая феноменальная “живучесть” этого типа измерителей.
Вольтметр действующих значений (среднеквадратичный) показывает величину напряжения, пропорциональную реальной долговременной мощности сигнала, его “тепловой эквивалент” И в самом деле, лучшие RMS-вольтметры построены именно с использованием термопреобразователей : исследуемое напряжение нагревает термоэлемент, по температуре которого и судят о величине напряжения.
Однако, как вы понимаете, нагрев термоэлемента - дело долгое, измеритель получается крайне инерционным, и применять его для оценки звуковых сигналов - занятие неблагодарное. Другое дело - измерение напряжения шумов.
Запомните!
Измерять уровень шумов аппаратуры можно ТОЛЬКО среднеквадратичным вольтметром! И никаким иным!
При использовании любых других - ошибки в результатах (из-за стохастического характера шумов) абсолютно непредсказуемы!
И вот теперь, постепенно, мы добрались до пикового вольтметра, который в подавляющем большинстве случаев как раз и служит измерителем уровней звуковых сигналов в профессиональной аппаратуре. Однако он в “чистом виде” малопригоден для работы, так как, реагируя даже на самые короткие пики сигнала, будет давать постоянно завышенные показания, а фонограмма при этом будет тихой. Как же быть?
Выход был найден в некотором (намеренном) “ухудшении” параметров измерителя - таким образом, что отдельные, “очень уж короткие” пики сигналов он как-бы “перестал видеть”. Для этого в схему измерителя были введены специальные интегрирующие зарядно-разрядные цепочки, определяющие динамические характеристики прибора. Такие измерители получили название “квазипиковые”, и вот они-то на самом деле и являются теми измерителями, с которыми мы имеем дело в повседневной практике.
Запомните!
Самые первые квазипиковые измерители имели время интеграции 60 миллисекунд, что примерно соответствует инерционности человеческого слуха. Время интеграции - это величина, определяющая быстродействие измерителя - или, иначе говоря - длительность тех коротких пиков сигнала, которые измеритель еще “видит”. Более короткие сигналы измеритель, конечно, тоже “видит” - но плохо(слабо).
Постепенно, с ростом технических требований к качеству записей, ужесточались и требования к измерителям уровней. Требовалось все большее отношение сигнал/шум, постоянно возрастал уровень записи (намагниченность ленты), и все меньшим становился запас по перегрузке. (А “цифра”, например не терпит даже малейших перегрузок. Вообще никаких!)
Чтобы более-менее надежно контролировать максимальные уровни сигналов, стали увеличивать быстродействие измерителей. Сначала время интеграции было уменьшено до 10 миллисекунд, а затем - и вовсе до 5 миллисекунд. (Считается, что искажения перегрузки с длительностью менее 5 мс ухо не замечает. Заметим от себя - это смотря КАКИЕ искажения. Цифровые - еще ох, как замечает!)
Но... За все приходится платить. В данном случае - за увеличение быстродействия измерителей - расплачиваться пришлось значительным увеличением разрыва между субъективно воспринимаемой громкостью звучания и показаниями индикаторов. Хотя в случае современной поп-музыки, до предела “сжатой”, закомпрессированной, этот разрыв не очень уж и велик.
Итак... 60-мс измерители удовлетворительно соответствуют субъективному восприятию громкости, но плохо показывают пики сигналов. 5-мс измерители хорошо индицируют пики, но их показания плохо коррелируют с громкостью звука. Как быть? Да очень просто. Решите - что вам, собственно, нужно контролировать?
Если вы обслуживаете передатчик - или другую линию связи - то для вас главное не допустить перегрузки. Смело выбирайте самый быстрый индикатор - и спокойно работайте. А о “плотности” звучания и других художественных особенностях - пусть голова болит у звукорежиссера программы.
А как ему, бедняге, быть?
Тупик? Пока еще нет. Есть два выхода.
Первый - это применение “двойных” индикаторов, которые показывают оба значения - и пиковое, и действующее. Они уже существуют и довольно широко применяются, хотя в их конструкции наличествует легкий оттенок вранья (нестрашного) : индикатор “Peak” реально квазипиковый (см. выше), а та часть индикатора, которая на самом деле показывает истинный RMS-уровень (да-да, есть и такие, только цена “кусается”), стыдливо, по инерции, именуется “VU”.
Но возможен и второй выход. Как знать - может быть, со временем, когда звукорежиссеры накопят достаточный опыт, снова повторится история с волюметром, только на этот раз “с точностью до наоборот”? А как Вы думаете?…
Михаил Чернецкий. E-mail :
LONG